今天依舊來介紹與Graph相關的演算法。
剩下幾天而已，加油!

最小生成樹（Minimum Spanning Tree）

生成樹（Spanning Tree）是圖論中的常見概念，它是原始圖的一個子圖，包含了原始圖中的所有節點，但只包括足夠多的邊，使得這個子圖成為一棵樹，而不包含任何環路。

特徵與概念

樹狀結構

樹狀結構

生成樹是一種樹狀結構，這表示它是一個無環圖，包含了所有原圖中的節點，並且連接這些節點的邊數正好是節點數減一。

連通性

生成樹確保原圖中的所有節點都是連通的。這意味著你可以從生成樹中的任意節點到達原圖中的任何其他節點。

生成樹的性質

生成樹包含了原圖的所有節點，但只包含原圖的一部分邊，以確保它沒有閉合的環路。生成樹是一種極小連通子圖，即在包含所有節點的情況下，具有最少的邊。

最小生成樹

在一個帶有權重的圖中，最小生成樹是一棵生成樹，其邊的權重總和是所有可能生成樹中最小的。常用的演算法來找到最小生成樹包括Prim演算法和Kruskal演算法。

尋找最小生成樹的演算法

尋找最小生成樹（Minimum Spanning Tree，MST）的問題是圖論中的經典問題，有多種演算法可以解決。以下為兩種常見的解決方法:

1. Prim's algorithm:以起始節點開始，逐步建立生成樹，每次選擇與生成樹相鄰且權重最小的邊所連接的節點，將其加入生成樹。 Prim演算法適用於稠密圖，其中邊的數量相對較多。
2. Kruskal's algorithm : 首先將圖中的所有邊依照權重從小到大排序，然後逐步將邊加入生成樹，但要確保生成樹保持無環。 Kruskal演算法適用於稀疏圖，其中邊的數量相對較少。

Prim's algorithm

遵循一個基本原則，即通過不斷選擇當前情況下的最優解，也就是權重最小的邊，來逐步構建最小生成樹。這確保最終生成樹是一棵樹，並且包含所有節點。
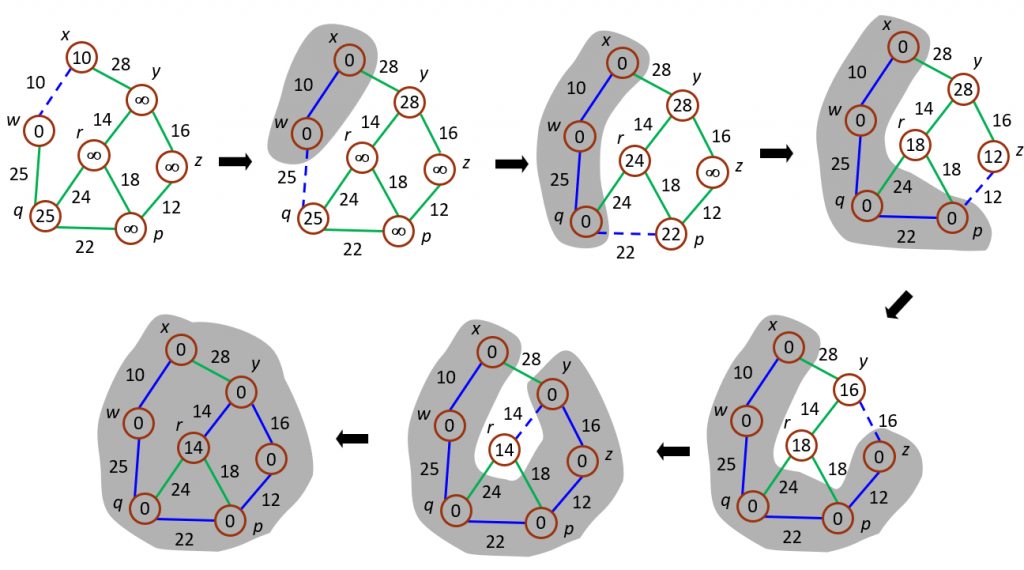
Prim演算法的基本步驟如下：

1. 初始化：首先，選擇一個起始節點，將其視為最小生成樹的一部分，同時初始化一個空的最小生成樹。
2. 找到最小邊：在已經選中的節點和未選中的節點之間，選擇一條權重最小的邊，並將其添加到最小生成樹中。這個邊的一個端點必須是已選中的節點，另一個端點必須是未選中的節點。
3. 重複步驟2：持續執行步驟2，直到最小生成樹包含了所有節點。

Prim演算法的時間複雜度通常為O(V^2)或O(E + V log V)，具體取決於實現方式。當圖的節點數較少時，V^2的實現方式可能更有效率。當圖的節點數較多時，使用堆（heap）數據結構以O(E + V log V)的複雜度實現可能更有效率。

Prim演算法常應用於解決連接網絡中找到最小成本的通信網絡佈線等問題，以及其他最小生成樹相關的應用。

圖解

程式碼

結構

// 定義一個邊的結構
struct Edge {
    char from, to;
    int weight;
    bool operator<(const Edge& other) const {
        return weight < other.weight;
    }
};

演算法

class Graph {
private:
    int vertices; // 點的個數
    vector<vector<int>> adjMatrix; // 鄰接矩陣
    vector<bool> visited; // 該點是否被訪問過
    vector<int> parent; // 該點的父節點
    vector<int> key; // 該點到最小生成樹的權重
public:
    Graph(int vertices) : vertices(vertices) {
        adjMatrix.resize(vertices);
        for (int i = 0; i < vertices; i++) {
            adjMatrix[i].resize(vertices, INF);
        }
        visited.resize(vertices, false);
        parent.resize(vertices, -1);
        key.resize(vertices, INF);
    }

    void prim(char start) {
        key[start - 'A'] = 0; // 起點的權重為0       
        for (int i = 0; i < vertices; i++) { // 遍歷所有點
            int minKey = INF;
            int minVertex = -1;
            for (int j = 0; j < vertices; j++) { // 找出最小權重的點
                if (!visited[j] && key[j] < minKey) {
                    minKey = key[j];
                    minVertex = j;
                }
            }
            visited[minVertex] = true;
            for (int j = 0; j < vertices; j++) { // 更新所有鄰接點的權重
                if (!visited[j] && adjMatrix[minVertex][j] < key[j]) {
                    key[j] = adjMatrix[minVertex][j];
                    parent[j] = minVertex;
                }
            }
        }
    }
};

Kruskal's algorithm

通過不斷選擇當前情況下的最優解，也就是權重最小的邊，並使用"不形成循環"的條件來確保最終生成樹是一棵樹，並且包含所有節點。
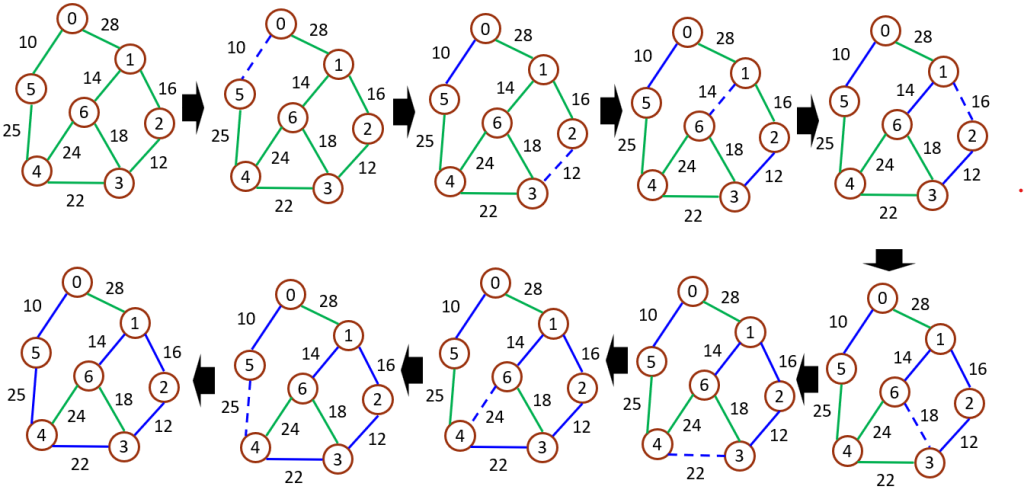
Kruskal演算法的主要步驟如下：

1. 初始化：首先，將所有的邊按照權重升序排序，同時初始化一個空的最小生成樹。
2. 依次選擇最小權重的邊：從排序後的邊中選擇權重最小的邊，然後將其添加到最小生成樹中。
3. 檢查是否形成循環：在添加新邊之後，檢查是否形成了循環。如果形成循環，則捨棄該邊，以確保生成樹的連通性，然後繼續選擇下一個最小權重的邊。
4. 重複步驟2和步驟3：持續執行步驟2和步驟3，直到最小生成樹包含所有節點或所有邊已經被考慮完。

Kruskal演算法是一種貪心算法，因為它優先選擇當前情況下的最優解，而不關心全局最優解。演算法的時間複雜度通常為O(E log E)，其中E是邊的數目。

Kruskal演算法在解決連接網絡中找到最小成本的通信網絡佈線等問題，以及其他最小生成樹相關的應用方面有廣泛的應用。

圖解

程式碼

結構

struct Edge {
    char from, to;
    int weight;
    bool operator<(const Edge& other) const {
        return weight < other.weight;
    }
};

演算法

class DisjointSet {
public:
    vector<char> parent; // parent[i]: i的父節點
    vector<int> rank; // rank[i]: i為根的樹的高度
    DisjointSet(int n) {
        parent.resize(n);
        rank.resize(n, 0);
        for(char i = 'A' ; i < 'A'+n ; i++)
            parent[i] = i;
    }
    char find(char x) { // 尋找x的根節點
        // 如果x的父節點不是自己，則繼續尋找
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }
    void merge(char x, char y) { // 合併x和y所在的集合
        int rootX = find(x);
        int rootY = find(y);
        
        if (rootX != rootY) {  // 如果兩個集合不在同一個集合中，則合併
            if (rank[rootX] > rank[rootY]) { // 以高度為基準合併
                parent[rootY] = rootX;
            } else if (rank[rootX] < rank[rootY]) {
                parent[rootX] = rootY;
            } else {
                parent[rootY] = rootX;
                rank[rootX]++;
            }
        }
    }
};

vector<Edge> kruskal(vector<Edge>& edges, int n) {
    sort(edges.begin(), edges.end(), [](const Edge& a, const Edge& b) {
        return a.weight < b.weight;
    });
    DisjointSet ds(n);
    vector<Edge> minimumSpanningTree;
    for (Edge& edge : edges) {// 如果兩個端點不在同一個集合，則加入最小生成樹
        if (ds.find(edge.from) != ds.find(edge.to)) {
            minimumSpanningTree.push_back(edge);
            ds.merge(edge.from, edge.to);
        }
    }
    return minimumSpanningTree;
}

Prim演算法和Kruskal演算法之比較

這個比較表突出了Prim演算法和Kruskal演算法之間的相似點和差異點。兩者都是貪心演算法，用於找到最小生成樹，但它們在邊的選擇方式和初始化方式等方面有所不同。選擇哪種演算法取決於您的具體需求和圖的性質。

有些人生難題確實很難克服，但有時候，只需要多一點勇氣，這已經是一種進步。